 Outlines of the PhD thesis.
Outlines of the PhD thesis.
 Outlines of the PhD thesis.
Outlines of the PhD thesis.
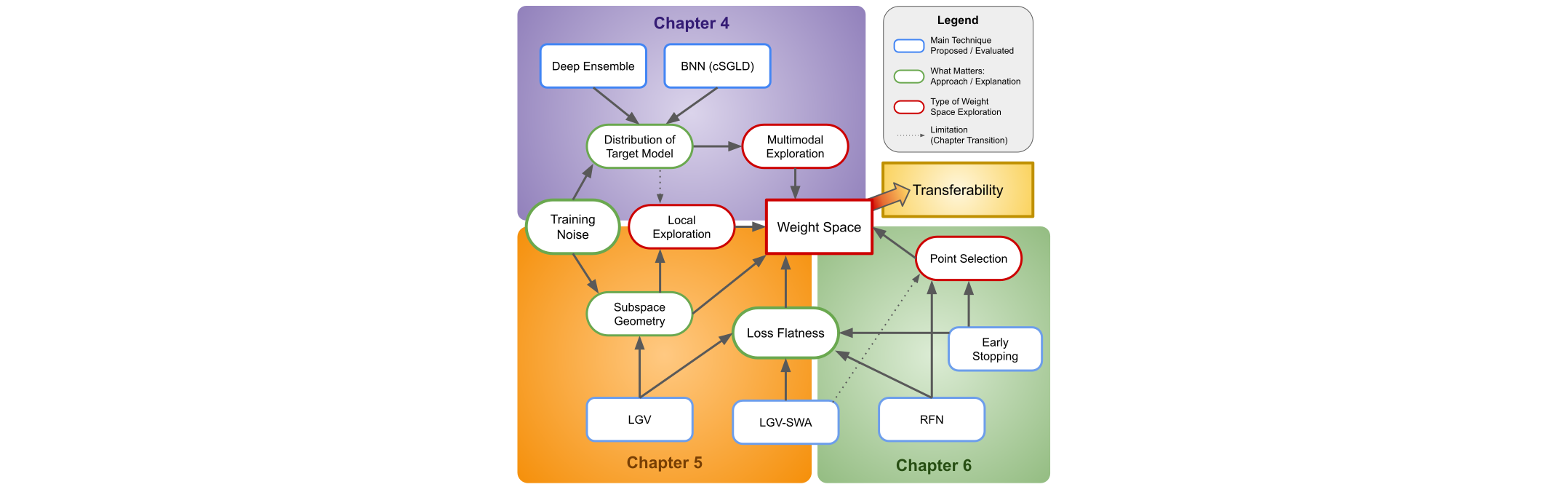
Despite state-of-the-art performance on natural data, Deep Neural Networks (DNNs) are highly vulnerable to adversarial examples, i.e., imperceptible, carefully crafted perturbations of inputs applied at test time. Adversarial examples can transfer: an adversarial example against one model is likely to be adversarial against another independently trained model. This dissertation investigates the characteristics of the surrogate weight space that lead to the transferability of adversarial examples. Our research covers three complementary aspects of the weight space exploration: the multimodal exploration to obtain multiple models from different vicinities, the local exploration to obtain multiple models in the same vicinity, and the point selection to obtain a single transferable representation. First, from a probabilistic perspective, we argue that transferability is fundamentally related to uncertainty. The unknown weights of the target DNN can be treated as random variables. Under a specified threat model, deep ensemble can produce a surrogate by sampling from the distribution of the target model. Unfortunately, deep ensembles are computationally expensive. We propose an efficient alternative by approximately sampling surrogate models from the posterior distribution using cSGLD, a state-of-the-art Bayesian deep learning technique. Our extensive experiments show that our approach improves and complements four attacks, three transferability techniques, and five more training methods significantly on ImageNet, CIFAR-10, and MNIST (up to 83.2 percentage points), while reducing training computations from 11.6 to 2.4 exaflops compared to deep ensemble on ImageNet. Second, we propose transferability from Large Geometric Vicinity (LGV), a new technique based on the local exploration of the weight space. LGV starts from a pretrained model and collects multiple weights in a few additional training epochs with a constant and high learning rate. LGV exploits two geometric properties that we relate to transferability. First, we show that LGV explores a flatter region of the weight space and generates flatter adversarial examples in the input space. We present the surrogate-target misalignment hypothesis to explain why flatness could increase transferability. Second, we show that the LGV weights span a dense weight subspace whose geometry is intrinsically connected to transferability. Through extensive experiments, we show that LGV alone outperforms all (combinations of) four established transferability techniques by 1.8 to 59.9 percentage points. Third, we investigate how to train a transferable representation, that is, a single model for transferability. First, we refute a common hypothesis from previous research to explain why early stopping improves transferability. We then establish links between transferability and the exploration dynamics of the weight space, in which early stopping has an inherent effect. More precisely, we observe that transferability peaks when the learning rate decays, which is also the time at which the sharpness of the loss significantly drops. This leads us to propose RFN, a new approach to transferability that minimises the sharpness of the loss during training. We show that by searching for large flat neighbourhoods, RFN always improves over early stopping (by up to 47 points of success rate) and is competitive to (if not better than) strong state-of-the-art baselines. Overall, our three complementary techniques provide an extensive and practical method to obtain highly transferable adversarial examples from the multimodal and local exploration of flatter vicinities in the weight space. Our probabilistic and geometric approaches demonstrate that the way to train the surrogate model has been overlooked, although both the training noise and the flatness of the loss landscape are important elements of transfer-based attacks.
The PhD thesis of Martin Gubri is titled “What Matters in Model Training to Transfer Adversarial Examples”. The thesis was defended the 21st of June in Luxembourg (Luxembourg) in front of the following jury members: